1

MLE1101 Tutorial 4 - Suggested Solutions

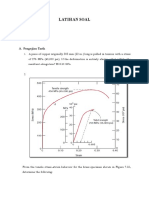
1. The following engineering stress-strain data were obtained at the beginning of a tensile test
for a 0.2%C plain-carbon steel.
(a) Plot the engineering stress-strain curve for these data.
(b) Determine the 0.2% offset yield stress for this steel.
(c) Determine the tensile elastic modulus of this steel. (Note that these data only give
the beginning part of the stress-strain curve.)
(Leave your answers in terms of pounds and inches.)

Engineering
Stress (kpsi)
Engineering
Strain (in./in.)
Engineering Stress
(kpsi)
Engineering
Strain (in./in.)
0 0 60 0.0035
15 0.0005 66 0.004
30 0.001 70 0.006
40 0.0015 72 0.008
50 0.0020

Solution:
(a)













(b) From figure in part (a), 0.2 percent yield stress = 66 kpsi.

(c) From figure in part (a),
7
30 1000 psi
tensile elastic modulus 3.0 10 psi
0.001
E
o
c

= = =








2

2. A 0.505-in.-diameter aluminum alloy test bar is subjected to a load of 25,000 lb
f
. If the
diameter of the bar is 0.490 in. at this load, determine (a) the engineering stress and strain
and (b) the true stress and strain. (Leave your answers in terms of pounds and inches.)

Solution:

( )
( )
2
2
2 0
0
2
2
2
0.505in
0.200in
4 4
0.490in
0.189in
4 4
i
i
d
A
d
A
t t
t t
= = =
= = =

Assume no volume change,
0 0 i i
A l Al = ,
(a)
2
0
25000lb
125,000 psi
0.200in
f
F
A
o = = =
c

= = = =
2
i 0 0
2
0 i
0.200in
1 1 0.058
0.189in
l l A
l A


(b)
2
25000lb
133,000 psi
0.189in
f
T
i
F
A
o = = =
c = = = =
2
0 i
2
0
0.200in
ln ln ln 0.057
0.189in
T
i
A l
l A



3. (a) Why do pure FCC metals like Ag and Cu have low values of critical resolved shear
stress t
c
?
(b) What is believed to be responsible for the high values of t
c
for HCP titanium?

Solution:
(a) For FCC metals like Ag and Cu, slip takes place on the close-packed {111} octahedral
planes and in the 110 < > close packed directions. Lower shear stress is required for
slip to occur in densely packed planes.

(b) The high t
c
values associated with HCP titanium is attributed to the mixed covalent
and metallic bonding with the atomic lattice structure.








3

4. A stress of 75 MPa is applied in the [001] direction on an FCC single crystal. Calculate (a) the
resolved shear stress acting on the (111)[101]

slip system and (b) the resolved shear stress
acting on the (111)[110]

slip system.

Solution:
(a) Referring to figures (i) to (iii) below, = 45, cos 54.7
3
a
a
| | = =
resolved shear stress, cos cos 75cos45 cos54.7 30.6MPa
r
t o | = = =

(b) Referring to figures (i) and (ii) below, = 90, cos 54.7
3
a
a
| | = =
resolved shear stress, cos cos 75cos90 cos54.7 0MPa
r
t o | = = =


4

5. A 70%Cu30%Zn brass wire is cold-drawn 20 percent to a diameter of 2.80 mm. The wire
is then further cold-drawn to a diameter of 2.45 mm. Definition of cold reduction is given as:

change in cross-sectional area
% cold reduction 100%
original cross-sectional area
=
(a) Calculate the total percent cold work that the wire undergoes.
(b) Estimate the wires tensile and yield strengths and elongation from Figure (a) in the
appendix.

Solution:
(a)
change in cross-sectional area
% cold reduction 100%
original cross-sectional area
=

( )
2
2
1 4 4
2
1 4
2 2 2
1 1 1
2.80mm
20% 100%
0.20 7.84mm 3.13mm
d
d
d d d
t t
t

=
= =


( ) ( )
( )
2 2
4 4
2
4
3.13mm 2.45mm
total % cold work 100% 38.75%
3.13mm
t t
t
(

= = (
(



(b) From fig. (a) in appendix, for cold work 39%,
Tensile Strength ~ 76 kpsi; Yield Strength ~ 64 kpsi and Elongation ~ 7 %


6. Derive the lever rule for the amount in weight percent of each phase in two-phase regions of
a binary phase diagram. Use a phase diagram in which two elements are completely soluble
in each other.

Solution:

















5

Recognise that the sum of weight fractions of liquid and solid phases is equal to 1
1
l S
X X + =
Considering the weight balance of B in the alloy as a whole and the sum of B in the two
phases, we arrive at:

( )
0
0
0
1
wt fraction of solid phase,
l l S S
S l S S
l
S
S l
w X w X w
w X w X w
w w
X
w w
= +
= +

Similarly,

wt fraction of liquid phase,

S o
l
S l
w w
X
w w



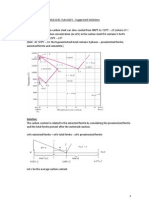
7. Consider the binary eutectic copper-silver phase diagram in the appendix (Figure b). Make
phase analyses of an 88wt%Ag12wt%Cu alloy at the temperatures (a) 1000
o
C, (b) 800
o
C, (c)
780
o
C + AT, (d) 780
o
C AT. AT is assumed to be less than 1
o
C. In the phase analyses, include:
(i) The phases present; (ii) The chemical compositions of the phases; (iii) The amounts of
each phase; (iv) Sketch the microstructure by using 2-cm-diameter circular fields.

Solution:
(a) at 1000
o
C,
Phases present: Liquid
Composition of phase: 88 wt% Ag
Amount of each phase:
wt% of liquid phase = 100%




(b) at 800
o
C,
Phases present: Liquid beta
Composition of phase: 78 wt% Ag in liquid phase 93 wt% Ag in beta phase
Amount of each phase:
93 88
wt% of liquid phase 100% 33.3%
93 78

= =

88 78
wt% of beta phase 100% 66.7%
93 78

= =

6

(c) at 780
o
C + AT,
Phases present: Liquid beta
Composition of phase: 71.9 wt% Ag in liquid phase 91.2 wt% Ag in beta phase
Amount of each phase:
91.2 88
wt% of liquid phase 100% 16.6%
91.2 71.9

= =

88 71.9
wt% of beta phase 100% 83.4%
91.2 71.9

= =

(d) at 780
o
C - AT,
Phases present: alpha beta
Composition of phase: 7.9 wt% Ag in alpha phase 91.2 wt% Ag in beta phase
Amount of each phase:
91.2 88
wt% of alpha phase 100% 3.8%
91.2 7.9

= =

88 7.9
wt% of beta phase 100% 96.2%
91.2 7.9

= =

8. Consider the binary peritectic iridium-osmium phase diagram in the appendix (Figure c).
Make phase analyses of a 70wt%Ir30wt%Os alloy at the temperatures (a) 2600
o
C, (b)
2665
o
C AT, (c) 2665
o
C + AT. AT is assumed to be less than 1
o
C. In the phase analyses,
include: (i) The phases present; (ii) The chemical compositions of the phases; (iii) The
amounts of each phase; (iv) Sketch the microstructure by using 2-cm-diameter circular
fields.

Solution:
(a) at 2600
o
C,
Phases present: Liquid alpha
Composition of phase: 18 wt% Os in liquid phase 40 wt% Os in alpha phase
Amount of each phase:

= =

40 30
wt% of liquid phase 100% 45.4%
40 18

= =

30 18
wt% of alpha phase 100% 54.6%
40 18







7

(b) at 2665
o
C - AT,
Phases present: Liquid alpha
Composition of phase: 23.0 wt% Os in liquid phase 43.0 wt% Os in alpha phase
Amount of each phase:
43 30
wt% of liquid phase 100% 65.0%
43 23

= =

30 23
wt% of alpha phase 100% 35.0%
43 23

= =

(c) at 2665
o
C + AT,
Phases present: Liquid beta
Composition of phase: 23.0 wt% Os in liquid phase 61.5 wt% Os in beta phase
Amount of each phase:
61.5 30
wt% of liquid phase 100% 81.8%
61.5 23

= =

30 23
wt% of beta phase 100% 18.2%
61.5 23

= =

9. Consider an Fe 4.2wt%Ni alloy (figure d in appendix) that is slowly cooled from 1550
o
C to
1450
o
C. Determine the amount of o phase and phase, respectively, at a temperature of
1517
o
C AT. Assume AT to less than 1
o
C.

Solution:

4.2 4
wt% of phase 100% 66.7%
4.3 4

= =

o

= =

4.3 4.2
wt% of phase 100% 33.3%
4.3 4