Professional Documents
Culture Documents
Drilling Hydraulics A
Uploaded by
sryn89Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Drilling Hydraulics A
Uploaded by
sryn89Copyright:
Available Formats
PETE 203
DRILLING ENGINEERING
Drilling Hydraulics
Drilling Hydraulics
Energy Balance
Flow Through Nozzles
Hydraulic Horsepower
Hydraulic Impact Force
Rheological Models
Optimum Bit Hydraulics
Nonstatic Well Conditions
Physical Laws:
Conservation of Mass
Conservation of energy
Conservation of momentum
Rheological Models
Newtonian
Bingham Plastic
Power Law
API Power-Law
Equations of State
Incompressible fluid
Slightly compressible fluid
Ideal gas
Real gas
Average Fluid Velocity
Pipe Flow Annular Flow
WHERE
v = average velocity, ft/s
q = flow rate, gal/min
d = internal diameter of pipe, in.
d
2
= internal diameter of outer pipe or borehole, in.
d
1
=external diameter of inner pipe, in.
2
448 . 2 d
q
v =
( )
2
1
2
2
448 . 2 d d
q
v
=
Law of Conservation of Energy
States that as a fluid flows
from point 1 to point 2:
Q W
v v D D g
V p V p E E
2
1
2
2 1 2
1 1 2 2 1 2
2
1
In the wellbore, in many cases Q = 0 (heat)
= constant
{
In practical field units
this equation simplifies to:
( )
( )
f p
p P v v
D D p p
A A +
+ =
2
1
2
2
4
1 2 1 2
10 * 074 . 8
052 . 0
p
1
and p
2
are pressures in psi
is density in lbm/gal.
v
1
and v
2
are velocities in ft/sec.
Ap
p
is pressure added by pump
between points 1 and 2 in psi
Ap
f
is frictional pressure loss in psi
D
1
and D
2
are depths in ft.
where
Determine the pressure at the
bottom of the drill collars, if
psi 000 , 3 p
in. 5 . 2
0 D
ft. 000 , 10 D
lbm/gal. 12
gal/min. 400 q
psi 1,400
p
1
2
= A
=
=
=
=
=
= A
DC
f
ID
p
(bottom of drill collars)
(mud pits)
Velocity in drill collars
) (in
(gal/min)
d 448 . 2
q
v
2 2
2
ft/sec 14 . 26
) 5 . 2 ( * 448 . 2
400
v
2
2
= =
Velocity in mud pits, v
1
0
400 , 1 000 , 3 6 . 6 240 , 6 0
400 , 1 000 , 3 ) 0 14 . 26 ( 12 * 10 * 8.074 -
0) - (10,000 12 * 052 . 0 0 p
P P ) v v ( 10 * 074 . 8
) D D ( 052 . 0 p p
2 2 4 -
2
f p
2
1
2
2
4 -
1 2 1 2
+ + =
+
+ =
A A +
+ =
Pressure at bottom of drill collars = 7,833 psig
NOTE: KE in collars
May be ignored in many cases
0
f p
P P v v
D D p p
A A +
+ =
) ( 10 * 074 . 8
) ( 052 . 0
2
1
2
2
4 -
1 2 1 2
0 P
v v 0 P
0 v D D
f
n 2 p
1 1 2
~ A
= = A
~ ~
Fluid Flow Through Nozzle
Assume:
A
=
=
4
n
2
n
4
1 2
10 * 074 . 8
p
v and
v 10 * 074 . 8 p p
If
{ } 95 . 0 c
10 * 074 . 8
p
c v
as written be may Equation
d
4
d n
~
A
=
0 = A
f
P
This accounts for all the losses in the nozzle.
Example: ft/sec 305
12 * 10 * 074 . 8
000 , 1
95 . 0 v
4
n
= =
For multiple nozzles in //
V
n
is the same for each nozzle
even if the d
n
varies!
This follows since Ap is the same across
each nozzle.
t
n
A 117 . 3
q
v =
2
t
2
d
2 -5
bit
A C
q 10 * 8.311
p
=
10 * 074 . 8
p
c v
4
d n
A
=
&
Hydraulic Horsepower
HHP of pump putting out 400 gpm at 3,000 psi = ?
Power
( )
p q P
A
q
A * p
t / s * F
work doing of rate
H
A =
A =
=
=
hp 700
1714
000 , 3 * 400
1714
p q
HHP = =
A
=
In field units:
Hydraulic Impact Force
What is the HHP Developed by bit?
Consider:
psi 169 , 1 p
lb/gal 12
gal/min 400 q
95 . 0 C
n
D
=
=
=
=
Impact = rate of change of momentum
( )
60 * 17 . 32
v q
v
t
m
t
mv
F
n
j
= A
|
.
|
\
|
A
=
A
A
=
psi 169 , 1 p
lb/gal 12
gal/min 400 q
95 . 0 C
n
D
=
=
=
=
lbf 820 169 , 1 * 12 400 * 95 . 0 * 01823 . 0 F
j
= =
p q c 01823 . 0 F
d j
A =
Newtonian Fluid Model
Shear stress = viscosity * shear rate
A
F
,
L
V
ally Experiment =
t =
Laminar Flow of Newtonian Fluids
A
F
L
V
=
Newtonian Fluid Model
In a Newtonian fluid the shear stress is directly
proportional to the shear rate (in laminar flow):
i.e.,
The constant of proportionality, is the
viscosity of the fluid and is independent of
shear rate.
|
.
|
\
|
=
sec
1
2
cm
dyne
t =
.
Newtonian Fluid Model
Viscosity may be expressed in poise or centipoise.
poise 0.01 centipoise 1
s cm
g
1
cm
s - dyne
1 poise 1
2
=
= =
2
cm
sec dyne -
t
=
.
Shear Stress vs. Shear Rate for a Newtonian
Fluid
Slope of line =
.
t =
Example - Newtonian Fluid
Example 4.16
Area of upper plate = 20 cm
2
Distance between plates = 1 cm
Force reqd to move upper plate at 10 cm/s
= 100 dynes.
What is fluid viscosity?
Example 4.16
poise 5 . 0
cm
s dyne
5 . 0
10
5
2
=
= =
1 -
2
sec 10/1
dynes/cm 20 / 100
/
/
rate shear
stress shear
= = =
L V
A F
cp 50 =
t =
Bingham Plastic Model
Bingham Plastic Model
- if
- if 0
if
y y p
y y
y y p
t < t t = t
t s t s t =
t > t t + = t
t and t
y
are often expressed in lbf/100 sq.ft
Power-Law Model
Power-Law Model
n = flow behavior index
K = consistency index
0 if K
0 if K
1 n
n
< =
> =
t
t
Rheological Models
1. Newtonian Fluid:
2. Bingham Plastic Fluid:
= t
rate shear
viscosity absolute
stress shear
=
=
=
+ = t t * ) (
p y
viscosity plastic
point yield
=
=
p
y
t
What if
y
= 0?
3. Power Law Fluid:
When n = 1, fluid is Newtonian and K =
We shall use power-law model(s) to
calculate pressure losses (mostly).
n
) ( K
= t
K =consistency index
n =flow behavior index
Rheological Models
Velocity Profiles
(laminar flow)
Fig. 4-26. Velocity profiles for laminar flow:
(a) pipe flow and (b) annular flow
It looks like concentric rings of fluid
telescoping down the pipe at different velocities
3D View of Laminar Flow in a pipe
- Newtonian Fluid
Summary of Laminar Flow Equations for Pipes and Annuli
Fig 4.33: Critical Reynolds number for
Bingham plastic fluids.
Fig 4.34: Fraction Factors for Power-law
fluid model.
Total Pump Pressure
Pressure loss in surf. equipment
Pressure loss in drill pipe
Pressure loss in drill collars
Pressure drop across the bit nozzles
Pressure loss in the annulus between the drill
collars and the hole wall
Pressure loss in the annulus between the drill
pipe and the hole wall
Hydrostatic pressure difference ( varies)
Total Pump Pressure
PUMP SC DP DC
B DCA DPA HYD
P P P P
P P P ( P )
= A + A + A +
A + A + A +
Types of Flow
Laminar Flow
Flow pattern is linear (no radial flow)
Velocity at wall is ZERO
Produces minimal hole erosion
Types of Flow - Laminar
Mud properties strongly affect
pressure losses
Is preferred flow type for annulus
(in vertical wells)
Laminar flow is sometimes referred to
as sheet flow, or layered flow:
* As the flow velocity increases, the flow type
changes from laminar to turbulent.
Types of Flow
Turbulent Flow
Flow pattern is random (flow in all directions)
Tends to produce hole erosion
Results in higher pressure losses
(takes more energy)
Provides excellent hole cleaningbut
Types of flow
Mud properties have little effect on pressure losses
Is the usual flow type inside the drill pipe and collars
Thin laminar boundary layer at the wall
Turbulent flow, contd
Fig. 4-30. Laminar and turbulent flow patterns in a circular pipe: (a) laminar
flow, (b) transition between laminar and turbulent flow and (c) turbulent flow
Turbulent Flow - Newtonian Fluid
The onset of turbulence in pipe flow is
characterized by the dimensionless group
known as the Reynolds number
d v
N
_
Re
=
d v 928
N
_
Re
=
In field units,
Turbulent Flow -
Newtonian Fluid
We often assume that fluid flow is
turbulent if N
re
> 2,100
cp. fluid, of viscosity
in I.D., pipe d
ft/s velocity, fluid avg. v
lbm/gal density, fluid where
_
=
=
=
=
d v 928
N
_
Re
=
P
PUMP
= AP
DP
+ AP
DC
+ AP
BIT NOZZLES
+ AP
DC/ANN
+ AP
DP/ANN
+ AP
HYD
Q = 280 gal/min
= 12.5 lb/gal
Pressure Drop Calculations
P
PUMP
"Friction" Pressures
0
500
1,000
1,500
2,000
2,500
0 5,000 10,000 15,000 20,000 25,000
Distance from Standpipe, ft
"
F
r
i
c
t
i
o
n
"
P
r
e
s
s
u
r
e
,
p
s
i
DRILLPIPE
DRILL COLLARS
BIT NOZZLES
ANNULUS
2103
Optimum Bit Hydraulics
Under what conditions do we get the
best hydraulic cleaning at the bit?
Maximum hydraulic horsepower?
Maximum impact force?
Both these items increase when the circulation
rate increases.
However, when the circulation rate increases,
so does the frictional pressure drop.
Jet Bit Nozzle Size Selection
Nozzle Size Selection for Optimum Bit
Hydraulics:
Max. Nozzle Velocity
Max. Bit Hydraulic Horsepower
Max. Jet Impact Force
Jet Bit Nozzle Size Selection
Proper bottom-hole cleaning
Will eliminate excessive regrinding of
drilled solids, and
Will result in improved penetration rates
Bottom-hole cleaning efficiency
Is achieved through proper selection of bit
nozzle sizes
Jet Bit Nozzle Size Selection
- Optimization -
Through nozzle size selection, optimization may
be based on maximizing one of the following:
Bit Nozzle Velocity
Bit Hydraulic Horsepower
Jet impact force
There is no general agreement on which of
these three parameters should be maximized.
Maximum Nozzle Velocity
From Eq. (4.31)
i.e.
so the bit pressure drop should be maximized in order
to obtain the maximum nozzle velocity
4
b
d n
10 * 074 . 8
P
C v
A
=
b n
P v A
Maximum Nozzle Velocity
This (maximization) will be achieved when the
surface pressure is maximized and the
frictional pressure loss everywhere is
minimized, i.e., when the flow rate is
minimized.
pressure. surface allowable maximum the and
rate n circulatio minimum the at
satisfied, are above 2 & 1 when maximized is v
n
Maximum Bit Hydraulic Horsepower
The hydraulic horsepower at the bit is
maximized when is maximized. q) p (
bit
A
d pump bit
p p p A A = A
where may be called the parasitic pressure
loss in the system (friction).
d
p A
bit d pump
p p p A + A = A
Maximum Bit Hydraulic Horsepower
. turbulent is flow the if
cq p p p p p p
75 . 1
dpa dca dc dp s d
= A + A + A + A + A = A
In general, where
m
d
cq p = A 2 m 0 s s
The parasitic pressure loss in the system,
Maximum Bit Hydraulic Horsepower
0 ) 1 ( p when 0
1714 1714
pump
1
= + A =
A
=
A
=
+
m
Hbit
m
pump
bit
Hbit
q m c
dq
dP
cq q p
q p
P
d pump bit
p p p A A = A
m
d
cq p = A
Maximum Bit Hydraulic Horsepower
when maximum is
1
1
p when ., .
) 1 ( p when ., .
d
pump
Hbit
pump
d
P
p
m
e i
p m e i
A
|
.
|
\
|
+
= A
A + = A
pump d
p
m
p A
|
.
|
\
|
+
= A
1
1
0 ) 1 ( p
pump
= + A
m
q m c
Maximum Jet Impact Force
The jet impact force is given by Eq. 4.37:
) ( c 0.01823
01823 . 0
d d pump
bit d j
p p q
p q c F
A A =
A =
Maximum Jet Impact Force
But parasitic pressure drop,
2 2
01823 . 0
+
A =
= A
m
d p d j
m
d
q c q p c F
cq p
) ( c 0.01823
d d pump j
p p q F A A =
Maximum Jet Impact Force
Upon differentiating, setting the first derivative
to zero, and solving the resulting quadratic
equation, it may be seen that the impact force is
maximized when,
p d
p
2 m
2
p A
+
= A
You might also like
- Drilling Basic 2001 ManualDocument286 pagesDrilling Basic 2001 Manualasset_kulmagambetov86% (7)
- Calculation Equations For Directional DrillingDocument79 pagesCalculation Equations For Directional Drillingmagdy199188% (8)
- Drilling Calculations CD Complete CourseDocument177 pagesDrilling Calculations CD Complete CourseIman100% (15)
- Formulas and Calculations for Drilling, Production, and Workover: All the Formulas You Need to Solve Drilling and Production ProblemsFrom EverandFormulas and Calculations for Drilling, Production, and Workover: All the Formulas You Need to Solve Drilling and Production ProblemsNo ratings yet
- Drilling application evaluate design bit hydraulicsDocument1 pageDrilling application evaluate design bit hydraulicsstevebeardsleyNo ratings yet
- OCTG NS-17 ABC of Hole CleaningDocument63 pagesOCTG NS-17 ABC of Hole CleaningDon Braithwaite100% (4)
- Optimization of Rig Hydraulics & Hole CleaningDocument60 pagesOptimization of Rig Hydraulics & Hole CleaningAbhinav Goyal100% (4)
- Drill String Design Group 3Document15 pagesDrill String Design Group 3Anusha AnuNo ratings yet
- CementingDocument4 pagesCementing07103091100% (2)
- Drilling Fluid PDFDocument68 pagesDrilling Fluid PDFShiela ONo ratings yet
- Applied Drilling Circulation Systems: Hydraulics, Calculations and ModelsFrom EverandApplied Drilling Circulation Systems: Hydraulics, Calculations and ModelsRating: 5 out of 5 stars5/5 (4)
- Drilling FluidDocument27 pagesDrilling Fluidmicnel jene100% (1)
- Drilling HydraulicDocument52 pagesDrilling HydraulicHeris Sitompul100% (1)
- Drilling Optimization PDFDocument22 pagesDrilling Optimization PDFRoyNo ratings yet
- Chapter 3 - Hydraulics and Hole Cleaning 2015Document86 pagesChapter 3 - Hydraulics and Hole Cleaning 2015Shalihan Mustafa0% (1)
- Best Practices Drilling 26 inDocument6 pagesBest Practices Drilling 26 inmanuelperdomotNo ratings yet
- Managed Pressure Drilling - TeaDocument50 pagesManaged Pressure Drilling - TeaCristhian LCNo ratings yet
- Primary Cementing CalculationsDocument40 pagesPrimary Cementing CalculationsMostafa ElghifaryNo ratings yet
- P and P Calc. AnDocument19 pagesP and P Calc. AnJaber AlbaajNo ratings yet
- Torque and Drag CalculationsDocument67 pagesTorque and Drag Calculationssivakmu100% (22)
- Common Rig MathDocument17 pagesCommon Rig MathSanjay Mishra86% (7)
- Ton MileDocument106 pagesTon MileAbdul Hameed OmarNo ratings yet
- All About MudDocument91 pagesAll About MudDavide Boreaneze100% (1)
- Torque and Drag CalculationsDocument67 pagesTorque and Drag CalculationsStalin ChugchilánNo ratings yet
- Wellbore Hydraulics, Pressure Drop CalculationsDocument85 pagesWellbore Hydraulics, Pressure Drop CalculationsDan Morrell100% (1)
- Drilling HydraulicsDocument22 pagesDrilling Hydraulicsdrilling moneytree100% (5)
- Casing Setting Depth DesignDocument26 pagesCasing Setting Depth Designehsan100% (1)
- Drilling HydraulicsDocument39 pagesDrilling HydraulicsAllbert Einstein100% (1)
- 12 - Hydraulic Calculations & MudpumpDocument1 page12 - Hydraulic Calculations & MudpumpJunaid MateenNo ratings yet
- Directional Drilling Calculation ExampleDocument10 pagesDirectional Drilling Calculation ExampleHeberth Desbloqueo100% (1)
- Cementing Basics EssentialsDocument53 pagesCementing Basics EssentialsUgochukwu Fidelis100% (1)
- Casing Design ExampleDocument42 pagesCasing Design ExampleSudish Bhat100% (1)
- Tubing Selection Factors for Optimizing Well ProductionDocument51 pagesTubing Selection Factors for Optimizing Well ProductionImam Zulkifli SNo ratings yet
- Hole CleaningDocument8 pagesHole Cleaninganon_850924421No ratings yet
- 6.mud Hydraulics Fundamentals PDFDocument11 pages6.mud Hydraulics Fundamentals PDFمعلومات ممتعه mohammedNo ratings yet
- Swab & Surge Pressure EstimationDocument1 pageSwab & Surge Pressure Estimationfrancisryan4519No ratings yet
- Drilling Operations Hole Cleaning DynamicsDocument38 pagesDrilling Operations Hole Cleaning DynamicsSAKNo ratings yet
- Introduction to Drilling Fluids - Functions, Properties & Systems (WBM/OBMDocument74 pagesIntroduction to Drilling Fluids - Functions, Properties & Systems (WBM/OBMSaul Pimentel100% (2)
- FIELD Site Vist Report-WET 2012-I Gede Suryana SDocument26 pagesFIELD Site Vist Report-WET 2012-I Gede Suryana Ssryn89No ratings yet
- Bit Hydraulics Optimization for Maximum Drilling PerformanceDocument23 pagesBit Hydraulics Optimization for Maximum Drilling PerformanceShakerMahmood100% (1)
- Practical Wellbore Hydraulics and Hole Cleaning: Unlock Faster, more Efficient, and Trouble-Free Drilling OperationsFrom EverandPractical Wellbore Hydraulics and Hole Cleaning: Unlock Faster, more Efficient, and Trouble-Free Drilling OperationsRating: 5 out of 5 stars5/5 (1)
- Casing and Casing Design 1Document60 pagesCasing and Casing Design 1Albert Wilson DavidNo ratings yet
- OCW Drilling Hydraulics LectureDocument59 pagesOCW Drilling Hydraulics Lecturefreelancer2earn100% (1)
- Wellbore Hydraulics, Pressure Drop CalculationsDocument85 pagesWellbore Hydraulics, Pressure Drop CalculationsNikhil ShahaneNo ratings yet
- Rahimov, MPDDocument102 pagesRahimov, MPDYassir HindiNo ratings yet
- Measurement While Drilling: Signal Analysis, Optimization and DesignFrom EverandMeasurement While Drilling: Signal Analysis, Optimization and DesignNo ratings yet
- EPC Level 4 Schedule PDFDocument7 pagesEPC Level 4 Schedule PDFEr Mangesh MohiteNo ratings yet
- Unit 01-08 - 3rd Ed. RDS (IADC-PETEX) - Circulating Systems PDFDocument59 pagesUnit 01-08 - 3rd Ed. RDS (IADC-PETEX) - Circulating Systems PDFRoyNo ratings yet
- Applied Gaseous Fluid Drilling Engineering: Design and Field Case StudiesFrom EverandApplied Gaseous Fluid Drilling Engineering: Design and Field Case StudiesNo ratings yet
- Swab and Surge Pressures SHBDocument1 pageSwab and Surge Pressures SHBstevebeardsleyNo ratings yet
- Bit Selection Guidelines PDFDocument225 pagesBit Selection Guidelines PDFSusan Li HB100% (2)
- Hole CleaningDocument39 pagesHole CleaningAmin100% (1)
- Shale Shaker and Drilling Fluids Systems:: Techniques and Technology for Improving Solids Control ManagementFrom EverandShale Shaker and Drilling Fluids Systems:: Techniques and Technology for Improving Solids Control ManagementRating: 4.5 out of 5 stars4.5/5 (2)
- Drilling HydraulicsDocument78 pagesDrilling HydraulicsKarlos Rdgz100% (1)
- Drill String Design 4.11Document23 pagesDrill String Design 4.11Ryan Tan Ping YiNo ratings yet
- Casing and Liners for Drilling and Completion: Design and ApplicationFrom EverandCasing and Liners for Drilling and Completion: Design and ApplicationRating: 5 out of 5 stars5/5 (3)
- Conceptual Physical Science: 5 EditionDocument72 pagesConceptual Physical Science: 5 EditionoperationmanagerNo ratings yet
- Full Report Kinematic ViscosityDocument11 pagesFull Report Kinematic ViscosityKyle Pong100% (1)
- What Does "Make A Statement" Mean?Document11 pagesWhat Does "Make A Statement" Mean?sryn89No ratings yet
- Pre TestDocument1 pagePre Testsryn89No ratings yet
- How To Make Your Own LED LightbulbsDocument9 pagesHow To Make Your Own LED Lightbulbssryn89No ratings yet
- QUIZDocument1 pageQUIZJant Erbert GarbosoNo ratings yet
- Orifice Meter Orifice Meter: - Introduction - Types - Construction - Working - Advantages - DisadvantagesDocument15 pagesOrifice Meter Orifice Meter: - Introduction - Types - Construction - Working - Advantages - DisadvantagesUmar DrazNo ratings yet
- Penyajian Data Kesetimbangan Menghitung Titik Uap dan EmbunDocument20 pagesPenyajian Data Kesetimbangan Menghitung Titik Uap dan Embunastri0% (1)
- Thermodynamics entropy calculationsDocument42 pagesThermodynamics entropy calculationsChristopher GalasNo ratings yet
- Thermo Exam QuestionsDocument4 pagesThermo Exam QuestionssiskieoNo ratings yet
- Van Der Waal's EquationDocument7 pagesVan Der Waal's EquationRosse KNo ratings yet
- Entropy in Thermodynamics and Info PDFDocument6 pagesEntropy in Thermodynamics and Info PDFsuudfiinNo ratings yet
- Analisis de Gas de Aceite de Transformador Utilizando Una Columna de Separacion Astm d3612 KasalabDocument2 pagesAnalisis de Gas de Aceite de Transformador Utilizando Una Columna de Separacion Astm d3612 KasalabJohnatan HernándezNo ratings yet
- Tutorial 3 - jan2015.PDF (Fluid Mech)Document4 pagesTutorial 3 - jan2015.PDF (Fluid Mech)pijechadNo ratings yet
- Lec 10 - The Ideal Gas Law and Kinetic TheoryDocument38 pagesLec 10 - The Ideal Gas Law and Kinetic TheoryAna ZarateNo ratings yet
- Vertical Knock Out Drum With Wire Mesh For NDocument1 pageVertical Knock Out Drum With Wire Mesh For NwdyouQNo ratings yet
- Mechanics of Fluids: Fluid Statics: 1Document6 pagesMechanics of Fluids: Fluid Statics: 1Ruben Alvin JosephNo ratings yet
- (Limno) Kuliah 9 (Do, Co2, PH)Document40 pages(Limno) Kuliah 9 (Do, Co2, PH)G-friendNo ratings yet
- WettabilityDocument8 pagesWettabilityAshish GuptaNo ratings yet
- Record of Hydrostatic TestDocument16 pagesRecord of Hydrostatic TestKrishna SaiNo ratings yet
- Exercise 1 Applications of Thermodynamics in Power Plant With AnswersDocument4 pagesExercise 1 Applications of Thermodynamics in Power Plant With AnswersKamil GuillerganNo ratings yet
- Topic 3, Lesson 1Document30 pagesTopic 3, Lesson 1George chaupi NyondoNo ratings yet
- BTech Engg PhysDocument10 pagesBTech Engg PhysAmith T KiniNo ratings yet
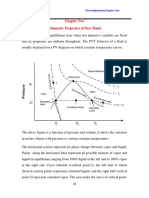
- Properties of Pure Substance and Steam Power Cycle Pure SubstanceDocument43 pagesProperties of Pure Substance and Steam Power Cycle Pure SubstanceSachin SinghNo ratings yet
- Purge Gas Purification and Recovery in Ammonia Plants: Process DescriptionDocument5 pagesPurge Gas Purification and Recovery in Ammonia Plants: Process DescriptionFerdian AziziNo ratings yet
- Senior General Chemistry 1 - Q1 - Module 11 For PrintingDocument36 pagesSenior General Chemistry 1 - Q1 - Module 11 For PrintingJiltonNo ratings yet
- Field SWT Report OO-4 (18-May-2023)Document6 pagesField SWT Report OO-4 (18-May-2023)حسن الجازويNo ratings yet
- PVT Behavior of Pure FluidsDocument18 pagesPVT Behavior of Pure Fluidsson gokuNo ratings yet
- Axial Fans and CompressorsDocument32 pagesAxial Fans and CompressorsAkshay DeshpandeNo ratings yet
- Multiphase Systems ExplainedDocument53 pagesMultiphase Systems Explainedعراقية KHNo ratings yet
- StatDocument70 pagesStatravitejabavandlaNo ratings yet
- Simple and Fractional Distillation Post Lab AbstractDocument4 pagesSimple and Fractional Distillation Post Lab AbstractAnvar MusokhonovNo ratings yet