Maximum and Minimum Values

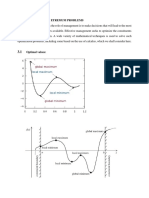
Absolute Maximum / Minimum Definition: A function f has an absolute maximum (also called global maximum) at c if f (c) f (x) for all x in its domain, D. The value f (c) is called the maximum value of f. A function f has an absolute minimum (or global minimum) at c if f (c) f (x) for all x in its domain. Such a value f (c) is called the minimum value of f. The maximum and minimum values of f are called the extreme values of f.

Local Maximum / Minimum Definition: A function f has a local maximum (or relative maximum) at c if f (c) f (x) when x near c. That is, f (c) f (x) for all x on some open interval containing c. Similarly, f has a local minimum (or relative minimum) at c if f (c) f (x) when x near c.

The Extreme Value Theorem (the existence of absolute maximum / minimum): If f is continuous on a closed interval [a, b] , then there exist (at least) a point c where f attains its maximum value, f (c), on the interval, and (at least) a point d where f attains its minimum value, f (d), on the interval. Comment: This means that if both of the following conditions: (1.) the interval is closed, and (2.) f is continuous on it, are met, then f is guaranteed to have (at least) one absolute maximum and one absolute minimum points on the interval. If either condition fails, then the existence of max / min points is not guaranteed.

Fermats Theorem (test for local extreme values): If f has a local maximum or minimum at c, and if f (c) exists, then f (c) = 0. Note 1: Therefore, it follows that a local extreme point can only occur at places where either f (x) = 0 or f (x) is undefined (i.e., either at a point where the tangent line is horizontal, or at a nondifferentiable point). Examples: f (x) = (x 2)2, at x = 2; g(x) =x, at x = 0. Note 2: The converse is not always true: the fact that f (c) = 0, or that f (c) does not exist, does NOT guarantee that c is a local extreme point of f. Example: f (x) = x3, at x = 0.

Definition: A critical point or critical number of a function f is a point x = c in the domain of f such that either f (c) = 0 or f (c) does not exist. Comment: The critical points are all the candidate points for local maximum / minimum of f . That is, every local extreme point is a critical point, but not every critical point is a local extreme point. Naturally, the max / min points of f have to be in the domain of f , i.e. they are points on the graph of f. Therefore, for example, if f is undefined at an infinite discontinuity then the point of discontinuity is not a critical point even though f does not exist there.

How to find the absolute maximum and minimum values of a continuous function f on a closed interval: 1. Find all critical points of f in the given interval. 2. Evaluate f at the critical point(s) found in step 1, as well as at the two endpoints of the interval. 3. The point(s) of the largest value of f is the absolute maximum(s), the point(s) of the smallest value is the absolute minimum(s).

Ex. Find the absolute maximum and minimum points of f (x) = 4 x2 on each of the intervals (i.) [3, 1], and (ii.) [2, 5]. f (x) = 2x f = 0 at x = 0 which is the only critical point because f is a polynomial, therefore, it has no nondifferentiable points. (i.) Evaluate f at the critical point 0 and the endpoints 3 and 1: f (3) = 5, f (0) = 4, f (1) = 3 Therefore, the absolute maximum point is (0, 4), and the absolute minimum point is (3, 5). (ii.) The critical point x = 0 is not in this interval, therefore, just evaluate f at the endpoints 2 and 5: f (2) = 0, f (5) = 21 Therefore, the absolute maximum point is (2, 0), and the absolute minimum point is (5, 21). Ex. Find the absolute maximum and minimum values of f (x) = x3 27x + 8 on the interval [0, 4]. Ans. abs max value of 8 at x = 0, abs min value of 46 at x = 3 Ex. Find the absolute maximum and minimum values of g(t) = t 3/5 on the interval [32, 1]. Ans. abs max value of 1 at t = 1, abs min value of 8 at t = 32