THE VIBRATING STRING PROBLEM

u ( x , t )

u(x,t)

B A x

0
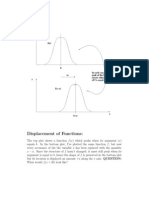
Figure 1 : Shape of String

Lx

x + x

Figure 2 : The forces acting on a small portion of string

Figure 1 and 2 , shows the transverse displacement u(x,t) of a string stretched along the x-axis between x = 0 and x = L. The string is free to vibrate in a fixed plane through the x-axis. The displacement u(x,t) might be obtained from the solution of a PDE that describes the motion of the string as a function of time. The PDE in this case is formulated from the physical law that is the conservation of momentum or force balance. The following assumptions are made to simplify the model. 1. The string is homogenous with constant mass per unit length . 2. The string is perfectly elastic and offers no resistance to bending so that the tension is tangent to the string. 3. The transverse vibrations of the strings are small and take place in a plane containing the xaxis, the xu-plane.

Let T denotes the magnitude of the string tension that is assumed to be constant throughout the motion since the change in the length of the string is negligible during its motion. Consider a small portion of the string between 2 points A and B located at x and x + x as shown in Figure 1 and 2. Let T1 and T2 be the tensions at the points A and B then |T1| = |T2| = T. Making a force balance in the vertical direction with positive pointing upward, we obtain

( (

) )

( (

) )

( (

) )

( (

) )

As,

then : [ ( ) ( )]

: and we get the equation for vibrating string Assume ( ) ( )

When

The expression

is known as the wave velocity and will be denoted as c, therefore the hyperbolic

equation that describes the string vibration is

STRING RELEASED AT REST EXAMPLE A perfectly elastic of equilibrium length 10 metres is released from rest in a configuration very close to that of a square pulse of unit height . between x=5 and x=6 that is : ( ) ( ) {

The string is clamped at both ends ( ) waves move on the string with speed c. Theres is no friction . Determine the subsequent evolution of the displacement ( ) of the string.

SOLUTION: First let us anticipate the response : The initial configuration looks like this , the pulse is just to the right of the centre of the string.

10

Two copies of the initial configuration, each half the height of the original, move off in opposite direction.

10

If the string were infinite , then the two waves would continue to recede from each other forever. At the fixed ends of the string, the waves bounce back, reflected.

10

They travel towards each other until they recombine into the negative of the original wave , just to the left of the centre of the string.

10

The second half of the cycle look like a time reversed version of the first half.

The general solution of the wave equation for With conditions : and

Both ends fixed for all time :

Initial configuration of string :

( )

String released from rest :

Is the fourier series : ( ) ( ( ) ( ) ) ( ) ( )

Here

and (

( )

( )

)]

)]

)]

* (

))+

REFERENCES

Schaum's Outline Series, Theory and Problems of Mechanical Vibrations [Schaum Publishing Co., 1964].

Stuart S. Antman, The American Mathematical Monthly, Vol 87 [ Mathematical Association of America Publishing.,1980]