Professional Documents
Culture Documents
Spherical Triangle
Uploaded by
Nikola PoljakCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Spherical Triangle
Uploaded by
Nikola PoljakCopyright:
Available Formats
Spherical Triangles and Girards Theorem
Abhijit Champanerkar
College of Staten Island, CUNY
MTH 329, Spring 2013
Spherical geometry
Let S
2
denote the unit sphere in R
3
i.e. the set of all unit vectors
i.e. the set {(x, y, z) R
3
| x
2
+y
2
+z
2
= 1 }.
A great circle in S
2
is a circle which divides the sphere in half. In
other words, a great circle is the interesection of S
2
with a plane
passing through the origin.
Spherical geometry
Let S
2
denote the unit sphere in R
3
i.e. the set of all unit vectors
i.e. the set {(x, y, z) R
3
| x
2
+y
2
+z
2
= 1 }.
A great circle in S
2
is a circle which divides the sphere in half. In
other words, a great circle is the interesection of S
2
with a plane
passing through the origin.
Spherical geometry
Let S
2
denote the unit sphere in R
3
i.e. the set of all unit vectors
i.e. the set {(x, y, z) R
3
| x
2
+y
2
+z
2
= 1 }.
A great circle in S
2
is a circle which divides the sphere in half. In
other words, a great circle is the interesection of S
2
with a plane
passing through the origin.
Great circles are straight lines
Great circles play the role of straight lines in spherical geometry.
Given two distinct points on S
2
, there is a great circle passing
through them obtained by the intersection of S
2
with the plane
passing through the origin and the two given points.
You can similarly verify the other three Euclids posulates for
geometry.
Great circles are straight lines
Great circles play the role of straight lines in spherical geometry.
Given two distinct points on S
2
, there is a great circle passing
through them obtained by the intersection of S
2
with the plane
passing through the origin and the two given points.
You can similarly verify the other three Euclids posulates for
geometry.
Great circles are straight lines
Great circles play the role of straight lines in spherical geometry.
Given two distinct points on S
2
, there is a great circle passing
through them obtained by the intersection of S
2
with the plane
passing through the origin and the two given points.
You can similarly verify the other three Euclids posulates for
geometry.
Diangles
Any two distinct great circles inter-
sect in two points which are nega-
tives of each other.
The angle between two great circles at an intersection point is the
angle between their respective planes.
A region bounded by two great circles is called a diangle.
The angle at both the vertices are equal. Both diangles bounded
by two great circles are congruent to each other.
Diangles
Any two distinct great circles inter-
sect in two points which are nega-
tives of each other.
The angle between two great circles at an intersection point is the
angle between their respective planes.
A region bounded by two great circles is called a diangle.
The angle at both the vertices are equal. Both diangles bounded
by two great circles are congruent to each other.
Diangles
Any two distinct great circles inter-
sect in two points which are nega-
tives of each other.
The angle between two great circles at an intersection point is the
angle between their respective planes.
A region bounded by two great circles is called a diangle.
The angle at both the vertices are equal. Both diangles bounded
by two great circles are congruent to each other.
Diangles
Any two distinct great circles inter-
sect in two points which are nega-
tives of each other.
The angle between two great circles at an intersection point is the
angle between their respective planes.
A region bounded by two great circles is called a diangle.
The angle at both the vertices are equal. Both diangles bounded
by two great circles are congruent to each other.
Area of a diangle
Proposition
Let be the angle of a diangle. Then the area of the diangle is 2.
Proof: The area of the diangle is proportional to its angle. Since
the area of the sphere, which is a diangle of angle 2, is 4, the
area of the diangle is 2.
Alternatively, one can compute this area directly as the area of a
surface of revolution of the curve z =
1 y
2
by an angle . This
area is given by the integral
1
1
z
1 + (z
)
2
dy.
If the radius of the sphere is r then the area of the diangle is 2r
2
.
This is very similar to the formula for the length of an arc of the
unit circle which subtends an angle is .
Area of a diangle
Proposition
Let be the angle of a diangle. Then the area of the diangle is 2.
Proof: The area of the diangle is proportional to its angle. Since
the area of the sphere, which is a diangle of angle 2, is 4, the
area of the diangle is 2.
Alternatively, one can compute this area directly as the area of a
surface of revolution of the curve z =
1 y
2
by an angle . This
area is given by the integral
1
1
z
1 + (z
)
2
dy.
If the radius of the sphere is r then the area of the diangle is 2r
2
.
This is very similar to the formula for the length of an arc of the
unit circle which subtends an angle is .
Area of a diangle
Proposition
Let be the angle of a diangle. Then the area of the diangle is 2.
Proof: The area of the diangle is proportional to its angle. Since
the area of the sphere, which is a diangle of angle 2, is 4, the
area of the diangle is 2.
Alternatively, one can compute this area directly as the area of a
surface of revolution of the curve z =
1 y
2
by an angle . This
area is given by the integral
1
1
z
1 + (z
)
2
dy.
If the radius of the sphere is r then the area of the diangle is 2r
2
.
This is very similar to the formula for the length of an arc of the
unit circle which subtends an angle is .
Area of a diangle
Proposition
Let be the angle of a diangle. Then the area of the diangle is 2.
Proof: The area of the diangle is proportional to its angle. Since
the area of the sphere, which is a diangle of angle 2, is 4, the
area of the diangle is 2.
Alternatively, one can compute this area directly as the area of a
surface of revolution of the curve z =
1 y
2
by an angle . This
area is given by the integral
1
1
z
1 + (z
)
2
dy.
If the radius of the sphere is r then the area of the diangle is 2r
2
.
This is very similar to the formula for the length of an arc of the
unit circle which subtends an angle is .
Spherical polygons
A spherical polygon is a polygon on S
2
whose sides are parts of
great circles.
More Examples. Take ballon, ball and draw on it.
Spherical Triangle
Spherical polygons
A spherical polygon is a polygon on S
2
whose sides are parts of
great circles.
More Examples. Take ballon, ball and draw on it.
Spherical Triangle
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Girards Theorem: Area of a spherical triangle
Girards Theorem
The area of a spherical triangle with angles , and is ++.
Proof:
Area of a spherical triangle
B
A
C
F
E
D
ABC as shown above is formed by the intersection of three great
circles.
Vertices A and D are antipodal to each other and hence have the
same angle. Similarly for vertices B, E and C, F. Hence the
triangles ABC and DEF are antipodal (opposite) triangles and
have the same area.
Assume angles at vertices A, B and C to be , and respectively.
Area of a spherical triangle
B
A
C
F
E
D
ABC R
AD
R
BE
R
CF
Let R
AD
, R
BE
and R
CF
denote pairs of diangles as shown. Then
ABC and DEF each gets counted in every diangle.
R
AD
R
BE
R
CF
= S
2
, Area(ABC) = Area(DEF) = X.
Area(S
2
) = Area(R
AD
) + Area(R
BE
) + Area(R
CF
) 4X
4 = 4 + 4 + 4 4X
X = + +
Area of a spherical triangle
B
A
C
F
E
D
ABC R
AD
R
BE
R
CF
Let R
AD
, R
BE
and R
CF
denote pairs of diangles as shown. Then
ABC and DEF each gets counted in every diangle.
R
AD
R
BE
R
CF
= S
2
, Area(ABC) = Area(DEF) = X.
Area(S
2
) = Area(R
AD
) + Area(R
BE
) + Area(R
CF
) 4X
4 = 4 + 4 + 4 4X
X = + +
Area of a spherical triangle
B
A
C
F
E
D
ABC R
AD
R
BE
R
CF
Let R
AD
, R
BE
and R
CF
denote pairs of diangles as shown. Then
ABC and DEF each gets counted in every diangle.
R
AD
R
BE
R
CF
= S
2
, Area(ABC) = Area(DEF) = X.
Area(S
2
) = Area(R
AD
) + Area(R
BE
) + Area(R
CF
) 4X
4 = 4 + 4 + 4 4X
X = + +
Area of a spherical polygon
Corollary
Let R be a spherical polygon with n vertices and n sides with interior
angles
1
, . . . ,
n
. Then Area(R) =
1
+ . . . +
n
(n 2).
Proof: Any polygon with n sides for n 4 can be divided into
n 2 triangles.
The result follows as the angles of these triangles add up to the
interior angles of the polygon.
Area of a spherical polygon
Corollary
Let R be a spherical polygon with n vertices and n sides with interior
angles
1
, . . . ,
n
. Then Area(R) =
1
+ . . . +
n
(n 2).
Proof: Any polygon with n sides for n 4 can be divided into
n 2 triangles.
The result follows as the angles of these triangles add up to the
interior angles of the polygon.
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5784)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (890)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (72)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- PY Vectors DR LeyDocument16 pagesPY Vectors DR LeyZurainiNo ratings yet
- BEARING AND NAVIGATION (Lesson 8)Document4 pagesBEARING AND NAVIGATION (Lesson 8)Teylan Ruzzel BartNo ratings yet
- Orient 3.4.2 User ManualDocument106 pagesOrient 3.4.2 User ManualnayemNo ratings yet
- Grade 5 Geometry: Choose Correct Answer(s) From The Given ChoicesDocument2 pagesGrade 5 Geometry: Choose Correct Answer(s) From The Given ChoicesAlbec Sagrado BallacarNo ratings yet
- 09 Circular MeasureDocument16 pages09 Circular MeasureQtravel GtnNo ratings yet
- Assign 1Document2 pagesAssign 1Jimwell Arnie Dela CruzNo ratings yet
- Radar Plotting 2Document14 pagesRadar Plotting 2Sto Cu100% (3)
- Drafting TerminologyDocument4 pagesDrafting Terminologyfaiyazansari100% (2)
- Theory of Survey Camp FinalDocument49 pagesTheory of Survey Camp FinalSujan Singh67% (3)
- PT g7 MathematicsDocument6 pagesPT g7 MathematicsLIWLIWA SUGUITAN100% (1)
- Circle Geometry TheoremsDocument12 pagesCircle Geometry TheoremsagentyikesNo ratings yet
- Mathematics Activity Sheet Quarter 4 - MELC 1Document11 pagesMathematics Activity Sheet Quarter 4 - MELC 1Rose BrazaNo ratings yet
- Grade 4 Math Identifies TrianglesDocument5 pagesGrade 4 Math Identifies TrianglesGizella Ann Dumdum100% (1)
- Rmo PDFDocument84 pagesRmo PDFarunNo ratings yet
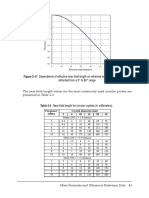
- Figure 2-17 Dependence of Effective Near-Field Length On Refracted Angle Longitudinal WavesDocument5 pagesFigure 2-17 Dependence of Effective Near-Field Length On Refracted Angle Longitudinal WavesKevin HuangNo ratings yet
- AQA IGCSE FM "Full Coverage": Trig in 2D and 3DDocument12 pagesAQA IGCSE FM "Full Coverage": Trig in 2D and 3DEinsteinNo ratings yet
- 4037 01 AdditionalMathematics ECR v1.1Document68 pages4037 01 AdditionalMathematics ECR v1.1Currect OrangeNo ratings yet
- General Physics 1 Q2 Week 1Document33 pagesGeneral Physics 1 Q2 Week 1Cyrelle FacunNo ratings yet
- 1 Find The Shaded Area in Each of The Following Circles. Leave Your Answers in Terms of Where AppropriateDocument4 pages1 Find The Shaded Area in Each of The Following Circles. Leave Your Answers in Terms of Where AppropriateboobooNo ratings yet
- Maths Test - 5 For Target/Fresher (19-08-2020) : Single Correct QuestionsDocument4 pagesMaths Test - 5 For Target/Fresher (19-08-2020) : Single Correct QuestionsJaya BNo ratings yet
- Egstar3 0-Southab PDFDocument92 pagesEgstar3 0-Southab PDFAli Zitouna HamedNo ratings yet
- N FSJPQ 3 K 16 Ut Ur Hja Dy UDocument14 pagesN FSJPQ 3 K 16 Ut Ur Hja Dy UVikas KumarNo ratings yet
- Mid Term Examination Model Question Paper 2022Document13 pagesMid Term Examination Model Question Paper 2022Sunil KumarNo ratings yet
- IXL - Singapore Primary 6 Maths CurriculumDocument4 pagesIXL - Singapore Primary 6 Maths CurriculumMichael ChanNo ratings yet
- 11P 3 Motion in A Plane PDFDocument67 pages11P 3 Motion in A Plane PDFAnkur SoniNo ratings yet
- Surveying Assignment - Traverse - Chapter1Document2 pagesSurveying Assignment - Traverse - Chapter1Nishchal SigdelNo ratings yet
- NIOSH Lifting EquationDocument33 pagesNIOSH Lifting EquationjabaprabuNo ratings yet
- Q-1 Part-2Document68 pagesQ-1 Part-2Pratap NNo ratings yet
- Surveying Measurements Probable ValuesDocument2 pagesSurveying Measurements Probable ValuesEarl averzosaNo ratings yet
- CE G2 Module No. 2 TrigonometryDocument1 pageCE G2 Module No. 2 TrigonometryDaniela CaguioaNo ratings yet