Professional Documents
Culture Documents
Chapter 9 (IESL)
Uploaded by
Muhammed IfkazCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Chapter 9 (IESL)
Uploaded by
Muhammed IfkazCopyright:
Available Formats
Chapter 10: The Stability of Linear Feedback Systems
10.1. Introduction
Stability of closed-loop feedback systems is central to control system design. A stable system should
exhibit a bounded output if the corresponding input is bounded. This is known as bounded-input-
bounded-output stability. The stability of a feedback system is directly related to the location of the
roots of the characteristic equation of the system transfer function and to the location of the Eigen
values of the system matrix for a system in state variable format. The Routh-Hurwitz method is
introduced as a useful tool for assessing system stability. The technique allows us to compute the
number of roots of the characteristic equation in the right half plane without actually computing the
values of the roots. This gives us a design method for determining values of certain system parameters
that will lead to closed-loop stability. For stable systems, that will introduce the notion of relative
stability, which allows us to characterize the degree of stability.
10.2. The concept of stability
When considering the design and analysis of feedback control systems, stability is of the greatest
importance. From a practical point of view, a closed-loop feedback system that is unstable is of little
value. As with all such general statements, there are exceptions; but for our purposes, that will declare
that all control designs must result in a closed-loop stable system. Many physical systems are naturally
open-loop unstable, and some systems are even designed to be open-loop unstable. Most modern
fighter aircraft are open-loop unstable by design, and without active feedback control assisting the pilot,
they cannot fly. Active control is introduced by engineers to stabilize the unstable system that is, the
aircraft, so that other considerations, such as transient performance, can be addressed. Using feedback,
system that can stabilize unstable systems and then with a sensible selection of controller parameters,
that can adjust the transient performance. For open-loop stable systems still use feedback to adjust the
closed-loop performance to meet the design specifications. These specifications take the form of
steady-state tracking errors, percent overshoot, settling time, time to peak, and the other indices.
By those parameters can be say that a closed-loop feedback system is either stable or it is not stable.
This type of stable/not stable characterization is referred to as absolute stability. A system possessing
absolute stability is called a stable system; the label of absolute is dropped. Given that a closed-loop
system is stable, that can further characterize the degree of stability. This is referred to as relative
EE4001: Control Systems I | Chapter 10 1
stability. The pioneers of aircraft design were familiar with the notion of relative stability the more
stable an aircraft was, the more difficult it was to maneuver. One outcome of the relative instability of
modern fighter aircraft is high maneuverability. A fighter aircraft is less stable than a commercial
transport; hence it can maneuver more quickly. In fact, the motions of a fighter aircraft can be quite
violent to the "passengers." That can determine that a system is stable (in the absolute sense) by
determining that all transfer function poles lie in the left-half s-plane, or equivalently, that all the Eigen
values of the system matrix A lie in the left-half s-plane. Given that all the poles (or Eigen values) are in
the left-half .v-plane, we investigate relative-stability by examining the relative locations of the poles (or
Eigen values).
A stable system is defined as a system with a bounded (limited) system response. That is, if the system
is subjected to a bounded input or disturbance and the response is bounded in magnitude, the system is
said to be stable.
A stable system is a dynamic system with a bounded response to a bounded input
The concept of stability can be illustrated by considering a right circular cone placed on a plane
horizontal surface. If the cone is resting on its base and is tipped slightly, it returns to its original
equilibrium position. This position and response are said to be stable. If the cone rests on its side and is
displaced slightly, it rolls with no tendency to leave the position on its side. This position is designated as
the neutral stability. On the other hand, if the cone is placed on its tip and released, it falls onto its side.
This position is said to be unstable. These three positions are shown in figure 10.1.
Figure 10.1: The stability of cone
EE4001: Control Systems I | Chapter 10 2
The stability of a dynamic system is defined in a similar manner. The response to a displacement, or
initial condition, will result in either a decreasing, neutral, or increasing response.
The location in the s-plane of the poles of a system indicates the resulting transient response. The poles
in the left-hand portion of the s-plane result in a decreasing response for disturbance inputs. Similarly,
poles on the -axis and in the right-hand plane result in a neutral and an increasing response,
respectively, for a disturbance input. This division of the -plane is shown in figure 10.2. Clearly, the
poles of desirable dynamic systems must lie in the left-hand portion of the -plane.
Figure 10.2: Stability in the -plane
A common example of the potential destabilizing effect of feedback is that of feedback hi-audio
amplifier and speaker systems used for public address in auditoriums. In this case, a loudspeaker
produces an audio signal that is an amplified version of the sounds picked up by a microphone. In
addition to other audio inputs, the sound coming from the speaker itself may be sensed by the
microphone. The strength of this particular signal depends upon the distance between the loudspeaker
and the microphone. Because of the attenuating properties of air, a larger distance will cause a weaker
signal to reach the microphone. Due to the finite propagation speed of sound waves, there will also be a
time delay between the signal produced by the loudspeaker and the signal sensed by the microphone.
In this case, the output from the feedback path is added to the external input. This is an example of
positive feedback.
As the distance between the loudspeaker and the microphone decreases, that find that if the
microphone is placed too close to the speaker, then the system will be unstable. The result of this
instability is an excessive amplification and distortion of audio signals and an oscillatory squeal.
EE4001: Control Systems I | Chapter 10 3
In terms of linear systems, we recognize that the stability requirement may be defined in terms of the
location of the poles of the closed-loop transfer function. The closed-loop system transfer function is
written as follow.
( ) ∏ ( + )
( )= =
( ) ∏ ( + )∏ ( +2 +( + ))
Where ( ) = ∆( ) = 0 is the characteristic equation whose roots are the poles of the closed-loop
system. The output response for an impulse function input (when = 0) is then
1
( )= + sin( + )
Where and are constants that depend on , , , and . To obtain a bounded response,
the poles of the closed-loop system must be in the left-hand portion of the -plane. Thus, a necessary
and sufficient condition for a feedback system to be stable is that all the poles of the system transfer
function have negative real parts. A system is stable if all the poles of the transfer function are in the
left-hand -plane. A system is not stable if not all the roots are in the left-hand plane. If the
characteristic equation has simple roots on the imaginary axis ( -axis) with all other roots in the left
half-plane, the steady-state output will be sustained oscillations for a bounded input, unless the input is
a sinusoid (which is bounded) whose frequency is equal to the magnitude of the -axis roots. For this
case, the output becomes unbounded. Such a system is called marginally stable, since only certain
bounded inputs (sinusoids of the frequency of the poles) will cause the output to become unbounded.
For an unstable system, the characteristic equation has at least one root in the right half of the -plane
or repeated roots; for this case, the output will become unbounded for any input.
EE4001: Control Systems I | Chapter 10 4
You might also like
- GCE OL 2019 MathsDocument12 pagesGCE OL 2019 MathsMuhammed IfkazNo ratings yet
- Jpupnfhz FZPJK Juk : NM M NDocument16 pagesJpupnfhz FZPJK Juk : NM M NMuhammed IfkazNo ratings yet
- Thodai Nigalthgavu 11 IDocument16 pagesThodai Nigalthgavu 11 IMuhammed Ifkaz100% (1)
- 0 B88 y YURTDglaak Z5 BL Et Q04 WD XMDocument7 pages0 B88 y YURTDglaak Z5 BL Et Q04 WD XMMuhammed IfkazNo ratings yet
- Understanding SONAR: Its History, Types and ApplicationsDocument14 pagesUnderstanding SONAR: Its History, Types and Applicationsmagalhaespaulo565No ratings yet
- Grade 11 Maths Unit CollectionDocument24 pagesGrade 11 Maths Unit CollectionMuhammed IfkazNo ratings yet
- Sonar Application: DSP ProjectDocument27 pagesSonar Application: DSP ProjectMuhammed IfkazNo ratings yet
- Module4 CausationDocument8 pagesModule4 CausationMuhammed IfkazNo ratings yet
- Activity 02 commands and shells guideDocument31 pagesActivity 02 commands and shells guideMuhammed IfkazNo ratings yet
- First Ministers Advisory Group On Human Rights Leadership Final Report For PublicationDocument79 pagesFirst Ministers Advisory Group On Human Rights Leadership Final Report For PublicationMuhammed IfkazNo ratings yet
- Sri Lankan CaseDocument7 pagesSri Lankan CasePradinath VinothNo ratings yet
- Power Systems ReportDocument7 pagesPower Systems ReportMuhammed IfkazNo ratings yet
- 3 (AB + AC + AD ) 4 (AH + AK ) VDF FHL Lf. 12Document7 pages3 (AB + AC + AD ) 4 (AH + AK ) VDF FHL Lf. 12Muhammed IfkazNo ratings yet
- Court Appeal Addresses False ImplicationDocument14 pagesCourt Appeal Addresses False ImplicationMuhammed IfkazNo ratings yet
- Fy TPG NGHJJ Juhjug GJ Jpu (Cau Ju) G Gapw RPG Gupl Ir General Certificate of Education (Adv. Level) Practice TestDocument3 pagesFy TPG NGHJJ Juhjug GJ Jpu (Cau Ju) G Gapw RPG Gupl Ir General Certificate of Education (Adv. Level) Practice TestMuhammed IfkazNo ratings yet
- Grade 11 SC Essay EM FinalDocument4 pagesGrade 11 SC Essay EM FinalMuhammed IfkazNo ratings yet
- Fy TPG NGHJJ Juhjug GJ Jpu (Cau Ju) G Gapw RPG Gupl Ir General Certificate of Education (Adv. Level) Practice TestDocument3 pagesFy TPG NGHJJ Juhjug GJ Jpu (Cau Ju) G Gapw RPG Gupl Ir General Certificate of Education (Adv. Level) Practice TestMuhammed IfkazNo ratings yet
- TOL Mat Paper12 2013Document11 pagesTOL Mat Paper12 2013SinthuNathanNo ratings yet
- Tutorial 2Document3 pagesTutorial 2Muhammed IfkazNo ratings yet
- NEW Biology L3Document21 pagesNEW Biology L3Muhammed IfkazNo ratings yet
- Vectors: Intensive Course P.L. Chathurika SilvaDocument11 pagesVectors: Intensive Course P.L. Chathurika SilvaMuhammed IfkazNo ratings yet
- Computer Networks Lab CorrectedDocument19 pagesComputer Networks Lab CorrectedMuhammed IfkazNo ratings yet
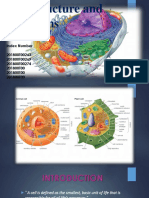
- CELLDocument19 pagesCELLMuhammed IfkazNo ratings yet
- GR 11 Science EM Paper IIDocument9 pagesGR 11 Science EM Paper IIMuhammed IfkazNo ratings yet
- sg11 Sci 1st TP Sbaragamu 2 2018Document12 pagessg11 Sci 1st TP Sbaragamu 2 2018Muhammed IfkazNo ratings yet
- Eg11 Sci TP NP 2016Document19 pagesEg11 Sci TP NP 2016Muhammed IfkazNo ratings yet
- UntitledDocument8 pagesUntitledMuhammed IfkazNo ratings yet
- Computer Networks LabDocument5 pagesComputer Networks LabMuhammed IfkazNo ratings yet
- Tutorial 2Document3 pagesTutorial 2Muhammed IfkazNo ratings yet
- FT 1001 2018 1 LMSDocument143 pagesFT 1001 2018 1 LMSMuhammed IfkazNo ratings yet
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (890)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Unit-3 Activity Planning and Risk Management The Objectives of Activity Planning Feasibility AssessmentDocument21 pagesUnit-3 Activity Planning and Risk Management The Objectives of Activity Planning Feasibility AssessmentzoeNo ratings yet
- Es Lab Manual-JntukDocument22 pagesEs Lab Manual-JntukMelissa GuerraNo ratings yet
- Bbcode TS3 PDFDocument1 pageBbcode TS3 PDFRoberto MicroNo ratings yet
- Analytical Fleet Maintenance Management: 3rd EditionDocument1 pageAnalytical Fleet Maintenance Management: 3rd EditionAnas R. Abu KashefNo ratings yet
- FIBER BILL STATEMENTDocument3 pagesFIBER BILL STATEMENTAnusha GodavarthyNo ratings yet
- Identifying Your Oracle Database Release NumberDocument2 pagesIdentifying Your Oracle Database Release Numberకృష్ణమోహన్ రెడ్డి గోపిరెడ్డిNo ratings yet
- A Study On Brand Awareness of Radhas Ayurvedic Soap ForRadhas Ayurvedic Soap WorksDocument2 pagesA Study On Brand Awareness of Radhas Ayurvedic Soap ForRadhas Ayurvedic Soap WorksnimishaNo ratings yet
- 1997 Vol 23 No 2 1001 AbstractDocument1 page1997 Vol 23 No 2 1001 AbstractFatih KantaşNo ratings yet
- HOCHIKI UL CatalogueDocument16 pagesHOCHIKI UL Cataloguearyan sharmaNo ratings yet
- Cabling Guide V1.0Document6 pagesCabling Guide V1.0nguyen vuNo ratings yet
- CSE 451: Operating Systems Semaphores and MonitorsDocument30 pagesCSE 451: Operating Systems Semaphores and MonitorsrinspdNo ratings yet
- Compiler Da2Document14 pagesCompiler Da2John WelshNo ratings yet
- Insync Cloud Editions Datasheet Druva PDFDocument4 pagesInsync Cloud Editions Datasheet Druva PDFAnkush AdlakhaNo ratings yet
- ERPSCM MM SRVServiceEntrySheet 180915 0417 1152Document7 pagesERPSCM MM SRVServiceEntrySheet 180915 0417 1152ronnzaaNo ratings yet
- Node JSDocument4 pagesNode JS12002040701186No ratings yet
- High Performance Hmi Scada Improves Efficiency Ge DecemberDocument53 pagesHigh Performance Hmi Scada Improves Efficiency Ge DecemberAnh Tuan Nguyen100% (1)
- Cisco Aironet 1140 Series Getting Started GuideDocument34 pagesCisco Aironet 1140 Series Getting Started GuideDmitryNo ratings yet
- BL-Exportation de Waybill (Centre) - 2023020813300000050468Document66 pagesBL-Exportation de Waybill (Centre) - 2023020813300000050468Khadija AkenouNo ratings yet
- John 1990, Price: $59.95.: Graphical Models in Applied Multivariate StatisticsDocument1 pageJohn 1990, Price: $59.95.: Graphical Models in Applied Multivariate StatisticsAqibAnsariNo ratings yet
- Real-Time Monitoring and Performance Harvesting For Grid-Connected PV System - A Case in SharjahDocument5 pagesReal-Time Monitoring and Performance Harvesting For Grid-Connected PV System - A Case in SharjahNeethu Elizabeth MichaelNo ratings yet
- U14 InclassDocument24 pagesU14 InclassImron MashuriNo ratings yet
- Help - Mens Work Jacket Mock UpDocument8 pagesHelp - Mens Work Jacket Mock UpMuhammad Zen WawazerNo ratings yet
- Resumen de Datasheet PIC18LF45K50Document75 pagesResumen de Datasheet PIC18LF45K50José Rafael Córdova RangelNo ratings yet
- Test 17Document23 pagesTest 17Joe StoneNo ratings yet
- Free Change Proposal Template PowerPoint DownloadDocument3 pagesFree Change Proposal Template PowerPoint DownloadbiniNo ratings yet
- Single Code Page Conversion Guide to UnicodeDocument22 pagesSingle Code Page Conversion Guide to Unicodezahid9486No ratings yet
- Pointers To Study 2nd Grading Grade 78 1Document8 pagesPointers To Study 2nd Grading Grade 78 1Val Alec TuballaNo ratings yet
- Xerox Phaser 3100 MFP Reman EngDocument15 pagesXerox Phaser 3100 MFP Reman EngPreduta MonicaNo ratings yet
- Bind Variables and Execute ImmediateDocument2 pagesBind Variables and Execute ImmediateSukh VirNo ratings yet
- Anirudh Internship Report On Web Development TraningDocument31 pagesAnirudh Internship Report On Web Development TraningShanu MishraNo ratings yet