Poisson Distribution

Attributes of a Poisson Experiment: A Poisson experiment is a statistical experiment that has the following properties: The experiment results in outcomes that can be classified as successes or failures. The average number of successes () that occurs in a specified region is known. The probability that a success will occur is proportional to the size of the region. The probability that a success will occur in an extremely small region is virtually zero. Note that the specified region could take many forms. For instance, it could be a length, an area, a volume, a period of time, etc. Notation The following notation is helpful, when we talk about the Poisson distribution. e: A constant equal to approximately 2.71828. (Actually, e is the base of the natural logarithm system.) : The mean number of successes that occur in a specified region. x: The actual number of successes that occur in a specified region. P(x; ): The Poisson probability that exactly x successes occur in a Poisson experiment, when the mean number of successes is . Poisson Distribution A Poisson random variable is the number of successes that result from a Poisson experiment. The probability distribution of a Poisson random variable is called a Poisson distribution. Given the mean number of successes () that occur in a specified region, we can compute the Poisson probability based on the following formula: Poisson Formula. Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is . Then, the Poisson probability is: P(x; ) = (e-) (x) / x! where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828. The Poisson distribution has the following properties: The mean of the distribution is equal to . The variance is also equal to . Example 1:The average number of homes sold by the Acme Realty company is 2 homes per day. What is the probability that exactly 3 homes will be sold tomorrow? This is a Poisson experiment in which we know the following: = 2; since 2 homes are sold per day, on average. x = 3; since we want to find the likelihood that 3 homes will be sold tomorrow. e = 2.71828; since e is a constant equal to approximately 2.71828. We plug these values into the Poisson formula as follows: P(x; ) = (e-) (x) / x! P(3; 2) = (2.71828-2) (23) / 3! P(3; 2) = (0.13534) (8) / 6 P(3; 2) = 0.180 Thus, the probability of selling 3 homes tomorrow is 0.180 .

Cumulative Poisson Probability A cumulative Poisson probability refers to the probability that the Poisson random variable is greater than some specified lower limit and less than some specified upper limit.

Example 2: Suppose the average number of lions seen on a 1-day safari is 5. What is the probability that tourists will see fewer than four lions on the next 1-day safari? This is a Poisson experiment in which we know the following: = 5; since 5 lions are seen per safari, on average. x = 0, 1, 2, or 3; since we want to find the likelihood that tourists will see fewer than 4 lions; that is, we want the probability that they will see 0, 1, 2, or 3 lions. e = 2.71828; since e is a constant equal to approximately 2.71828. To solve this problem, we need to find the probability that tourists will see 0, 1, 2, or 3 lions. Thus, we need to calculate the sum of four probabilities: P(0; 5) + P(1; 5) + P(2; 5) + P(3; 5). To compute this sum, we use the Poisson formula: P(x < 3, 5) = P(0; 5) + P(1; 5) + P(2; 5) + P(3; 5) P(x < 3, 5) = [ (e-5)(50) / 0! ] + [ (e-5)(51) / 1! ] + [ (e-5)(52) / 2! ] + [ (e-5)(53) / 3! ] P(x < 3, 5) = [ (0.006738)(1) / 1 ] + [ (0.006738)(5) / 1 ] + [ (0.006738)(25) / 2 ] + [ (0.006738)(125) / 6 ] P(x < 3, 5) = [ 0.0067 ] + [ 0.03369 ] + [ 0.084224 ] + [ 0.140375 ] P(x < 3, 5) = 0.2650 Thus, the probability of seeing at no more than 3 lions is 0.2650. Example 3:: On an average Friday, a waitress gets no tip from 5 customers. Find the probability that she will get no tip from 7 customers this Friday. The waitress averages 5 customers that leave no tip on Fridays: = 5. Random Variable : The number of customers that leave her no tip this Friday. We are interested in P(X = 7). Example 4: During a typical football game, a coach can expect 3.2 injuries. Find the probability that the team will have at most 1 injury in this game. A coach can expect 3.2 injuries : = 3.2. Random Variable: The number of injuries the team has in this game. We are interested in .

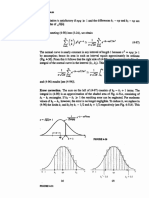
Example 5: A small life insurance company has determined that on the average it receives 6 death claims per day. Find the probability that the company receives at least seven death claims on a randomly selected day. P(x 7) = 1 - P(x 6) = 0.393697

Example 6: The number of traffic accidents that occurs on a particular stretch of road during a month follows a Poisson distribution with a mean of 9.4. Find the probability that less than two accidents will occur on this stretch of road during a randomly selected month. P(x < 2) = P(x = 0) + P(x = 1) = 0.000860

Poisson distribution examples

1. The number of road construction projects that take place at any one time in a certain city follows a Poisson distribution with a mean of 3. Find the probability that exactly five road construction projects are currently taking place in this city. (0.100819) 2. The number of road construction projects that take place at any one time in a certain city follows a Poisson distribution with a mean of 7. Find the probability that more than four road construction projects are currently taking place in the city. (0.827008) 3. The number of traffic accidents that occur on a particular stretch of road during a month follows a Poisson distribution with a mean of 7.6. Find the probability that less than three accidents will occur next month on this stretch of road. (0.018757) 4. The number of traffic accidents that occur on a particular stretch of road during a month follows a Poisson distribution with a mean of 7. Find the probability of observing exactly three accidents on this stretch of road next month. (0.052129) 5. The number of traffic accidents that occur on a particular stretch of road during a month follows a Poisson distribution with a mean of 6.8. Find the probability that the next two months will both result in four accidents each occurring on this stretch of road. (0.009846) 6. Suppose the number of babies born during an 8-hour shift at a hospital's maternity wing follows a Poisson distribution with a mean of 6 an hour. Find the probability that five babies are born during a particular 1-hour period in this maternity wing. (0.160623) 7. The university policy department must write, on average, five tickets per day to keep department revenues at budgeted levels. Suppose the number of tickets written per day follows a Poisson distribution with a mean of 8.8 tickets per day. Find the probability that less than six tickets are written on a randomly selected day from this distribution. (0.128387) 8. The number of goals scored at State College hockey games follows a Poisson distribution with a mean of 3 goals per game. Find the probability that each of four randomly selected State College hockey games resulted in six goals being scored. (.00000546)