Professional Documents
Culture Documents
20090316100324molecule and Condensed
Uploaded by
Gee FizieyOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
20090316100324molecule and Condensed
Uploaded by
Gee FizieyCopyright:
Available Formats
MOLECULE AND SOLID
Chapter Outline
1. Types of Molecular Bonds
2. Structure of Solids
3. Energy Bands
4. Free-Electron Model of Metals
5. Semiconductors and its Devices
42.1 Types of Molecular Bonds
The ionic bond is an interaction between
oppositely charged ionized atoms.
The ionization energy or ionization potential
of an element is the energy require to
remove a valence electron from its neutral
atom.
When the two oppositely charged ions are
brought together by their mutual attraction,
the magnitude of their negative potential
energy is determined by how closely they
can approach each other (Fig. 42.1).
42.1 Types of Molecular Bonds
Fig. 42.1
U(r) proportional to 1/r as for point
charges. As r decrease, the charge
clouds of the two atoms overlap and the
force becomes less attractive . If r is
less than the equilibrium separation r
0
,
the force is repulsive
Example 42.1 Electric potential
energy of the NaCl molecule
Find the electric potential energy of Na
+
and Cl
-
ions separated by 0.24 nm if they can be
treated as point charges.
Example 42.1 (SOLN)
Identify and Set Up
We use Eq. (23.9) from Section 23.1, which
tells us that the electric potential energy of two
point charges q and q
0
separated by a distance
r is U = qq
0
/4t}
0
r.
Example 42.1 (SOLN)
Execute
The two charges are q = +e (for Na
+
) and q
0
= -
e (for Cl
-
), and the separation is r = 0.24 nm =
0.24 x 10
-9
m. From Eq. (23.9),
2 19 2
9 2 2
9
0 0
19
1 (1.6 10 )
(9.0 10 / )
4
0.24 10
9.6 10 6.0
e C
U N m C
r
m
J eV
t
= =
e
= =
42.1 Types of Molecular Bonds
The covalent bond is characterized by a
more egalitarian participation of the two
atoms than occurs with the ionic bond.
As two separate atoms come together, the
net attraction of the electrons for each
proton more than balances the repulsion of
the two protons and of the two electrons
(Fig. 42.2).
42.1 Types of Molecular Bonds
Fig. 42.2
42.1 Types of Molecular Bonds
An atom with
several electrons in
its outermost shell
can form several
covalent bonds
(Fig. 42.3).
Fig. 42.3
42.1 Types of Molecular Bonds
The Van der Waals bond, is an interaction
between the electric dipole moments of atoms or
molecules; typical energies are 0.1eV or less
The bonding of water molecules in the liquid and
solid states results partly from dipole-dipole
interactions
Not much thermal agitation energy is needed to
break these weak bonds
Usually those substances exist in the liquid and solid states
at very low temperatures
42.1 Types of Molecular Bonds
Hydrogen bonds is a proton (H+ ion) gets between
two atoms, polarizing them and attracting them by
means of the induced dipoles (usually less than
0.5eV)
This bond is unique to hydrogen-containing
compounds because only because only hydrogen
has a singly ionized state with no remaining
electron cloud.
It plays as a role in many organic molecules
Cross-linking of polymer chains (polyethylene)
Cross-linking bonding between the strands of the double-
helix DNA molecule.
In the structure of ice
42.3 Structure of Solids
The term condensed matter includes both solids and
liquids.
Adjacent atoms attract one another until their outer
electron charge clouds begin to overlap significantly.
In crystalline solids, atoms have long-range order where
a recurring pattern of atomic positions extend over many
atoms.
In amorphous solids and liquids, there is only short-
range order (correlations between neighboring atoms or
molecules) (Fig. 42.10).
For instance, common window glass, polystyrene and
cotton candy are amorphous solids.
42.3 Structure of Solids
The amorphous
structure of
glassy Silica
(SiO2). No long
range order is
present, however
there is local
ordering with
respect to the
tetrahedral
arrangement of
Oxygen (O) atoms
around the Silicon
(Si) atoms.
Fig. 42.10
42.3 Structure of Solids
A crystal lattice is a repeating pattern of
mathematical points that extends throughout
space:
Fig. 42.11
42.3 Structure of Solids
The bcc and fcc
structures are two
common simple
crystal structures.
Fig. 42.12
42.3 Structure of Solids
Fig. 42.13 shows a
representation of
the fcc structure of
sodium chloride
(NaCl, ordinary
salt).
Fig. 42.13
42.3 Structure of Solids
Another crystal type is the metallic crystal, where
one or more of the outermost electrons in each
atom become detached from the parent atom
(leaving a position ion) and are free to move
through the crystal.
The corresponding electron wave functions extend
over many atoms
Thus a metallic crystal consists of an array of
positive ions immersed in a sea of freed electrons
whose attraction for the positive ions holds the
crystal together (Fig. 42.16).
42.3 Structure of Solids
Fig. 42.16
42.4 Energy Bands
As the distance between atoms decreases, the
energy levels spread into energy bands (Fig.
42.19).
Fig. 42.19
42.4 Energy Bands
Between adjacent energy bands are gaps
where there are no allowed energy levels.
The nature of the energy bands determines
whether the material is an electrical
insulator, a semiconductor, or a conductor.
Fig. 42.20
Example 42.6 Photoconductivity
in germanium
Even at room temperature, pure germanium
has an almost completely filled valence band
separated by a gap of 0.67 eV from an almost
completely empty conduction band. It is a poor
electrical conductor, but its conductivity
increases substantially when it is irradiated
with electromagnetic waves of certain
maximum wavelength. What maximum
wavelength is appropriate?
Example 42.6 (SOLN)
An electron at the top of the valence band can
absorb a photon with energy of 0.67 eV (no
less) and move to the bottom of the conduction
band, where it is a mobile charge. Thus the
maximum wavelength is
15 8
max
min
6
(4.136 10 )(3.00 10 / )
0.67
1.9 10 1900
hc eV s m s
E eV
m nm
= =
= =
42.5 Free-Electron Model of
Metals
The free-electron model assumes
that electrons are completely free
inside the metal and dont interact at
all with the ions or with each other, but
that there are infinite potential-energy
barriers at the surfaces.
This is the three-dimensional version
of the infinite square well (Fig. 42.21).
42.5 Free-Electron Model of
Metals
Fig. 42.21
42.5 Free-Electron Model of
Metals
The three-
dimensional space
can be represented
with coordinates
(n
x
, n
y
, n
z
).
Fig. 42.22
42.5 Free-Electron Model of
Metals
The density of states is then:
It is also important to determine how the electrons
are distributed among the various quantum states
at any given temperature.
42.5 Free-Electron Model of
Metals
Fig. 42.23 shows
the probability
distribution for
occupation of free-
electron energy
states at absolute
zero.
Fig. 42.23
42.5 Free-Electron Model of
Metals
The statistical distribution function that emerges
from the exclusion principle and the
indistinguishability requirement is the Fermi-Dirac
distribution:
E
f
energy of the highest occupied quantum state in
a system of fermions at absolute zero temperature
Fig. 42.24 shows graphs of Eq. (42.17) for several
temperatures.
42.5 Free-Electron Model of
Metals
Fig. 42.24
Example 42.7 Probabilities in
the free-electron model
For free electrons in a solid, at what energy is
the probability that a particular state is
occupied is equal to a) 0.01; b) 0.99?
Example 42.7 (SOLN)
Solving Eq. (42.17) for E, we get
a) When f(E) = 0.01,
A state 4.6kT above the Fermi level is
occupied only 1% of the time.
1
ln 1
( )
F
E E kT
f E
| |
= +
|
\ .
1
ln 1 4.6
0.01
F F
E E kT E kT
| |
= + = +
|
\ .
Example 42.7 (SOLN)
b) When f(E) = 0.99,
A state 4.6kT below the Fermi level is occupied
99% of the time.
1
ln 1 4.6
0.99
F F
E E kT E kT
| |
= + =
|
\ .
Example 42.7 (SOLN)
Evaluate
At very low temperatures, 4.6kT becomes very
small. Then levels even slightly below E
F
are
nearly always full, and levels even slightly
above E
F
nearly always empty (see Fig. 42.24).
In general, if the probability is P that a state
with an energy AE above E
F
is occupied, then
the probability is 1 P that a state AE below E
F
is occupied. We leave the proof as a problem
(Problem 42.46).
Example 42.8 The Fermi
energy in copper
At low temperatures, copper has a free-
electron concentration of 8.45 x 10
28
m
-3
. Using
the free-electron model, find the Fermi energy
for solid copper, and find the speed of an
electron with a kinetic energy equal to the
Fermi energy.
Example 42.8 (SOLN)
Identify and Set Up
Because copper is a solid conductor, its Fermi
energy changes very little with temperature
and we can safely use the expression for the
Fermi energy at absolute zero. We determine
the speed v
F
that corresponds to kinetic energy
E
F
using the familiar nonrelativistic formula for
kinetic energy.
Example 42.8 (SOLN)
Execute
Using the given value of n,
To find the corresponding speed v
F
, we use E
F
= mv
F
2
:
2/ 3 4/ 3 34 28 3 2/ 3
31
18
3 (1.055 10 )(8.45 10 )
2(9.11 10 )
1.126 10 7.03
F
J s m
E
kg
J eV
t
= =
18
6
31
2 2(1.126 10 )
1.57 10 /
9.11 10
F
F
E J
v m s
m
kg
= = =
Example 42.9 Free-electron gas
versus ideal gas
a) Find the average energy of the free
electrons in copper at absolute zero (Example
42.8). b) If the electrons behaved as an ideal
gas (Section 18.3) at room temperature, what
would be their average kinetic energy? What
would be the speed of an electron with this
kinetic energy?
Example 42.9 (SOLN)
Identify and Set Up
We use Eq. (42.22) to determine the average
kinetic energy of free electrons. If the electrons
behaved as a classical ideal gas with
temperature T, from Eq. (18.16) the average
kinetic energy per electron would be E
av
=
3/2kT; we use this relationship to determine the
energy and the speed asked for in part (b).
Example 42.9 (SOLN)
Execute
a) From Example 42.8, the Fermi energy in copper is
1.126 x 10
-18
J = 7.03 eV. According to Eq. (42.22), the
average energy is 3/5 of this, or 6.76 x 10
-19
J = 4.22
eV.
b) If the electrons behaved like an ideal gas at room
temperature (T = 20C = 293 K), the average energy
per electron would be
23
21
3 3
(1.381 10 / )(293 )
2 2
6.07 10 0.0379
av
E kT J K K
J eV
= =
= =
Example 42.9 (SOLN)
The speed of an electron with this kinetic
energy would be
21
5
31
2 2(6.07 10 )
1.15 10 /
9.11 10
av
E J
v m s
m
kg
= = =
42.6 Semiconductors
A semiconductor has an electrical
resistivity that is intermediate between those
of good conductors and of good insulators.
Example 42.10 Jumping the
energy gap
Consider a material with the band structure
described above, with its Fermi energy in the
middle of the gap (Fig. 42.25). Find the
probability that a state at the bottom of the
conduction band is occupied at a temperature
of 300 K if the band gap is a) 0.200 eV; b) 1.00
eV; c) 5.00 eV. Repeat the calculations for a
temperature of 310 K.
Example 42.10 Jumping the
energy gap
Fig. 42.25
Example 42.10 (SOLN)
Identify and Set Up
The Fermi-Dirac distribution function gives us
the probability that a state of energy E is
occupied at temperature T. Figure 42.25 shows
that the state of interest at the bottom of the
conduction band has energy E = E
F
+ E
g
/2, so
E E
F
= E
g
/2.
Example 42.10 (SOLN)
a)When E
g
= 0.200 eV,
With E
g
= 0.200 eV and T = 310 K, the
exponent is 3.74 and f(E) = 0.0231, a 13%
increase for a temperature rise of only 10 K.
5
3.87
0.100
3.87
(8.617 10 / )(300 )
1
( ) 0.0205
1
F
E E eV
kT
eV K K
f E
e
= =
= =
+
Example 42.10 (SOLN)
b) When E
g
=1.00 eV, both exponents are five times as large
as before, 19.3 and 18.7; the values of f(E) are 4.0 x 10
-9
and
7.4 x 10
-9
. In this case the probability nearly doubles with a
temperature rise of 10 K.
c) When E
g
= 5.0 eV, the exponents are 96.7 and 93.6, the
values of f(E) are 1.0 x 10
-42
and 2.3 x 10
-41
. The probability
increases by a factor of 23 for a 10-K temperature rise, but it is
still extremely small. Pure diamond, with a 5.47-eV band gap,
has essentially no electrons in the conduction band and is an
excellent insulator.
Example 42.10 (SOLN)
Evaluate
This example illustrates two important points. First, the
probability of finding an electron in a state at the
bottom of the conduction band is extremely sensitive to
the width of the band gap. When the gap is 0.20 eV the
chance is about 2%, but when it is 1.00 eV, the chance
is a few in a thousand million, and for a band gap of 5.0
eV it is essentially zero. Second, for any given band
gap the probability is very temperature dependent,
more so for large gaps than for small.
42.6 Semiconductors
When an electron is removed from a
covalent bond, it leaves a vacancy, called a
hole, behind.
An electron from a neighboring atom can
then move into this vacancy.
This hole can travel through the material
and serve as an additional current carrier
(Fig. 42.26).
42.6 Semiconductors
Fig. 42.26
42.6 Semiconductors
The deliberate
addition of impurity
elements is called
doping (Fig. 42.27).
If the conductivity is
due to negative
charge (electron)
motion, the material
is called an n-type
semiconductor.
Fig. 42.27
42.6 Semiconductors
If the conductivity is
due to positive
charge (hole)
motion, the material
is a p-type
semiconductor.
Fig. 42.28
42.7 Semiconductors Devices
In many semiconductor devices the
essential principle is the fact that the
conductivity of the material is controlled by
impurity concentrations, which can be varied
within wide limits from one region of a
device to another.
An example is the p-n junction at the
boundary between one region of a
semiconductor with p-type impurities and
another region containing n-type impurities
(Fig. 42.29).
42.7 Semiconductors Devices
Fig. 42.29
42.7 Semiconductors Devices
A p-n junction conducts much more readily in the
direction from p to n than the reverse.
Such a (mostly) one-way device is called a diode
rectifier.
The current through a p-n junction is given by:
42.7 Semiconductors Devices
If an electric field is in the direction from p to
n, this is the forward direction, and the
positive potential difference is called forward
bias.
If the electric field is reversed, the
corresponding negative potential difference
is called reverse bias.
Fig. 42.30 shows a p-n junction in
equilibrium, with no externally applied field
or potential difference.
42.7 Semiconductors Devices
Fig. 42.30
42.7 Semiconductors Devices
Fig. 42.31
Under forward bias, the electric field in the junction
region decreases.
42.7 Semiconductors Devices
Under reverse bias,
the potential-energy
difference between the
junction region
becomes greater than
at equilibrium (Fig.
42.32).
Large reverse bias will
lead to processes such
as avalanche
breakdown and Zener
breakdown.
Fig. 42.32
42.7 Semiconductors Devices
A bipolar junction transistor includes two p-n
junctions in a sandwich configuration,
which may be either p-n-p or n-p-n.
Such a p-n-p transistor is shown in Fig.
42.33.
42.7 Semiconductors Devices
Fig. 42.33
42.7 Semiconductors Devices
Another widely
used arrangement
is the common-
emitter circuit (Fig.
42.34).
Fig. 42.34
42.7 Semiconductors Devices
Fig. 42.35
The field-effect transistor is also an important type
of transistor.
Concept Summary
You might also like
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (890)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- Eternal Source of Energy in the Universe RevealedDocument4 pagesEternal Source of Energy in the Universe Revealeddag57No ratings yet
- Simple Harmonic MotionDocument13 pagesSimple Harmonic MotionAdid PunyaNo ratings yet
- Proposed Energy Efficiency Directive Standards AnalysisDocument6 pagesProposed Energy Efficiency Directive Standards AnalysisJose M. MartorellNo ratings yet
- SMK ST Anthony YFB 6102 Science Panel Form 2 Yearly Lesson Plan 2015Document2 pagesSMK ST Anthony YFB 6102 Science Panel Form 2 Yearly Lesson Plan 2015Gee FizieyNo ratings yet
- f1 c7 Heat 1Document47 pagesf1 c7 Heat 1qq235100% (3)
- Experiment 3.1.1Document7 pagesExperiment 3.1.1Gee FizieyNo ratings yet
- Physical Quantity SI Unit SymbolDocument2 pagesPhysical Quantity SI Unit SymbolGee FizieyNo ratings yet
- 5.1 Inert GasesDocument6 pages5.1 Inert GasesSuzilfarinda SamikNo ratings yet
- Physics Form 4 Chapter 1Document19 pagesPhysics Form 4 Chapter 1闷闷女孩No ratings yet
- Lesson 2: Sound Properties and Their PerceptionDocument5 pagesLesson 2: Sound Properties and Their PerceptionGee FizieyNo ratings yet
- Ionic Bonding in Halide SaltsDocument8 pagesIonic Bonding in Halide SaltsGee FizieyNo ratings yet
- Learning OutcomesDocument6 pagesLearning OutcomesGee FizieyNo ratings yet
- 3.enex General 070616Document23 pages3.enex General 070616Ropiudin EnergiNo ratings yet
- SREDocument8 pagesSREAlexandra ParaschivNo ratings yet
- Free Electron in Solids PDFDocument30 pagesFree Electron in Solids PDFTamara HerediaNo ratings yet
- College Physics 7th Ed Serway Chapter 11Document30 pagesCollege Physics 7th Ed Serway Chapter 11Jorge GomezNo ratings yet
- Contoh Soal Dan Penyelesain Ke2Document4 pagesContoh Soal Dan Penyelesain Ke2Siti HannaNo ratings yet
- Chapter - 2 - Energy - Energy Transfer and General Energy AnalysisDocument35 pagesChapter - 2 - Energy - Energy Transfer and General Energy AnalysisKarti ViveygenNo ratings yet
- Chapter 4 (Heat and Temperature)Document33 pagesChapter 4 (Heat and Temperature)QaisNo ratings yet
- ENGR 302 Energy and EnvironmentDocument4 pagesENGR 302 Energy and EnvironmentYuna AnjosNo ratings yet
- Pambudi 2017Document9 pagesPambudi 2017anjarNo ratings yet
- Digital Media NotesDocument2 pagesDigital Media Notesaspaps123No ratings yet
- Seminar Report On Fusion Power PlantDocument33 pagesSeminar Report On Fusion Power Plantnavin shukla100% (1)
- Chemring CM Renewable Energy ReportDocument47 pagesChemring CM Renewable Energy ReportEmily ButlerNo ratings yet
- 22 RNG PDFDocument41 pages22 RNG PDFJuan DomaniczkyNo ratings yet
- RERC Order SummaryDocument3 pagesRERC Order SummaryMonica MercadoNo ratings yet
- Physics II Problems PDFDocument1 pagePhysics II Problems PDFBOSS BOSSNo ratings yet
- Watermill To Microhydropower - EthiopiaDocument28 pagesWatermill To Microhydropower - Ethiopiafrezer_awolNo ratings yet
- Automatic Generation Control of Interconnected Power System With Diverse Sources of Power GenerationDocument15 pagesAutomatic Generation Control of Interconnected Power System With Diverse Sources of Power GenerationVahid SadeghiNo ratings yet
- Work Power and EnergyDocument6 pagesWork Power and EnergyshahidkakaNo ratings yet
- Energy Bands and Charge Carriers in SemiconductorsDocument7 pagesEnergy Bands and Charge Carriers in SemiconductorsSushil KumarNo ratings yet
- Conservation of Energy Lab AlternativeDocument3 pagesConservation of Energy Lab Alternativeapi-292550476No ratings yet
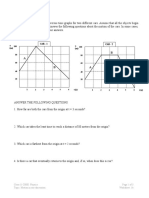
- Position vs Time Graphs of Two Cars AnalyzedDocument3 pagesPosition vs Time Graphs of Two Cars AnalyzedraghulNo ratings yet
- Programme FinalDocument24 pagesProgramme FinalabdulkarymNo ratings yet
- Krannich Solar Company and Product OverviewDocument17 pagesKrannich Solar Company and Product OverviewTayfun KoçakNo ratings yet
- Bohr's Model of The AtomDocument8 pagesBohr's Model of The AtomMuhammad Awais TariqNo ratings yet
- Powering The FutureDocument16 pagesPowering The Futureshanu104No ratings yet
- Contoh Pembuatan CVDocument2 pagesContoh Pembuatan CVAditia KurniawanNo ratings yet
- Maximizing Power Supply in BoholDocument5 pagesMaximizing Power Supply in BoholNelsonPolinarLaurdenNo ratings yet