Finite Potential Well

The potential energy is zero

(U(x) = 0) when the particle
is 0 < x < L (Region II)
The energy has a finite
value (U(x) = U) outside this
region, i.e. for x < 0 and x > L
(Regions I and III)
We also assume that energy
of the particle, E, is less than
the height of the barrier,
i.e. E < U
Finite Potential Well
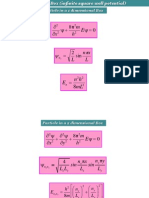
Schrdinger Equation


.I x < 0; U(x) = U


.II 0 < x < L; U(x) = 0


.III x > L; U(x) = 0
II
II
E
dx
d
m

=
2
2 2
2

I I
I
E U
dx
d
m

=
2
2 2
2

( )
( ) ( ) x E x x U
x
x
m

= +
c
c
) (
2
2
2 2

III III
III
E U
dx
d
m

=
2
2 2
2

Finite Potential Well: Region II

U(x) = 0
This is the same situation as
previously for infinite
potential well
The allowed wave functions
are sinusoidal
The general solution is

II
(x) = F sin kx + G cos kx
where F and G are constants

The boundary
conditions , however,
no longer require that
(x) be zero at the
ends of the well
Finite Potential Well: Regions I and III
The Schrdinger equation for these regions is


It can be re-written as


The general solution of this equation is
(x) = Ae
Cx
+ Be
-Cx
A and B are constants

E U
dx
d
m
=
2
2 2
2

2
2 2
2 2
2
) ( 2
where ,
) ( 2

E U m
C C
E U m
dx
d
=

Finite Potential Well Regions I and III

Requiring that wavefunction was finite at x
and x - , we can show that
In region I, B = 0, and
I
(x) = Ae
Cx
This is necessary to avoid an infinite value for
(x) for large negative values of x
In region III, A = 0, and
III
(x) = Be
-Cx
This is necessary to avoid an infinite value for
(x) for large positive values of x
Finite Potential Well
Thus, we have to equate
parts of the wavefunction
and its derivative at x = 0, L
This, together with
normalization condition,
allows to determine the
constants and the equation for
energy of the particle
The wavefunction and its derivative must be single-valued
for all x
There are only two points where the wavefunction might have more
than one value: x = 0 and x = L
( ) ( )
( ) ( ) L
dx
d
L
dx
d
L L
dx
d
dx
d
III II
III II
II I
II I
) ( ) (
0 0
) 0 ( ) 0 (




=
=
=
=
Finite Potential Well
Graphical Results for

(x)
Outside the potential
well, classical physics
forbids the presence of
the particle
Quantum mechanics
shows the wave function
decays exponentially to
approach zero
Finite Potential Well
Graphical Results for Probability Density, |

(x) |
2
The probability densities
for the lowest three
states are shown
The functions are
smooth at the
boundaries
Outside the box, the
probability to find the
particle decreases
exponentially, but it is
not zero!
Fig 3.15
From Principles of Electronic Materials
and Devices, Third Edition, S.O. Kasap
( McGraw-Hill, 2005)
x = 0 x = a
0
E
1
E
3
E
2
E
4
n = 1
n = 2
n = 3
n = 4
E
n
e
r
g
y
o
f
e
l
e
c
t
r
o
n
Energy levels in the well (x) sin(ntx/a)
Probability density |(x)|
2

4
0
a a
0
x
0 a
x
0
V
(
x
)
V = 0
Electron
V = 8 V = 8
Electron in a one-dimensional infinite PE well. The energy of the
electron is quantized. Possible wavefunctions and the probability
distributions for the electron are shown.
8